Исследование асимптотических свойств псевдорегулярных функций и обобщенных процессов восстановления

Суть научно-технической разработки состоит в исследовании асимптотического поведения псевдорегулярных функций и их аналогов в стохастическом анализе – обобщенных процессов восстановления, а также применении полученных результатов в теории случайных процессов, статистики случайных процессов, математическом анализе и математической физике.
В работе:
- получен ряд новых результатов про асимптотическое поведение последовательностей случайных величин и векторов с линейной регрессионной зависимостью. В частности, получены окончательные критерии сходимости рядов многомерных регрессионных последовательностей с постоянными матричными коэффициентами, а также установлены необходимые и достаточные условия усиленного закона больших чисел в форме Марцинкевича-Зигмунда для таких последовательностей;
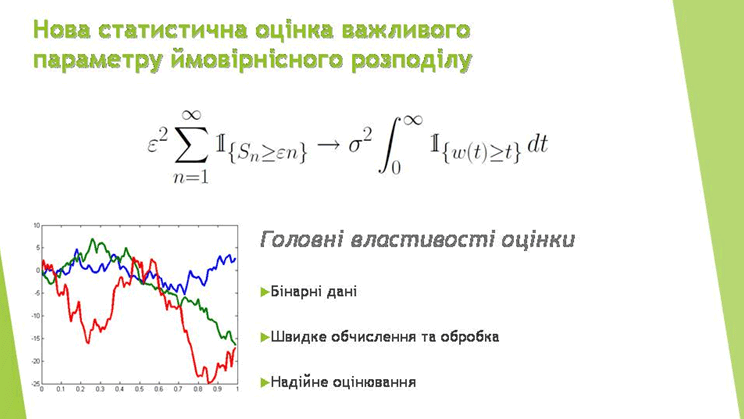
- существенно дополнены классические результаты теории полной сходимости для последовательностей независимых случайных величин и векторов. В частности, установлен критерий сходимости почти наверное эмпирических аналогов рядов Баума-Каца и Сюя-Роббинса с весами. Кроме того, найдены необходимые и достаточные условия существования конечных моментов таких эмпирических рядов;
- в теории гауссовских случайных процессов в обобщение классических результатов Дуба и Парка получено критерии эквивалентности общего гауссовского процесса броуновскому движению, броуновскому мосту и процессу Орнштэйна-Уленбека;
- дальнейшее развитие получила теория правильно меняющихся функций. В частности, в рамках этой теории исследовано класс комплекснозначных функций с невырожденными группами регулярных точек и доказаны аналоги классических теорем про изображения. В качестве иного обобщения рассмотрены матричнозначные правильно меняющиеся функции и доказаны теоремы про их регуляризацию;
- существенно расширено классическую теорию рекордов, основанную в работах А. Реньи. В частности, изучено асимптотическое поведение моментов рекордов и числа рекордов в так называемое -схеме;
- получены новые важные результаты в качественной теории стохастических дифференциальных уравнений. Для широкого класса таких уравнений исследовано асимптотическое поведение решений на бесконечности, а также условия, при которых это решение является асимптотически неслучайным. Эти результаты существенно обобщают классические теоремы Гихмана и Скорохода;
- в обобщение классических результатов теории восстановления исследовано асимптотическое поведение аналога функции восстановления для случайного блуждания в многомерном времени;
- рассмотрено обобщение стохастической модели паркования А. Реньи, которое позволяет различать водителей с разным опытом вождения. Для такой модели паркования описано асимптотическое поведение среднего количества припаркованных автомобилей;
- получено новые значительные результаты в нелинейном регрессионном анализе. В частности, исследовано асимптотическое распределение оценки Коэнкера-Бассета параметра нелинейной модели регрессии с сильно зависимым шумом;
- дальнейшее развитие получила теория дифференциальных уравнений в частных производных. Среди прочего, найдены новые условия классичности обобщенных решений начально–краевых и смешанных задач для линейных параболических уравнений второго и высших порядков. Эти условия сформулированы в терминах принадлежности правых частей уравнений некоторым пространствам Хермандера.