Формалізація комплексних методів нелінійного аналізу та оптимального керування складними розподіленими системами різної природи
Розроблено нові та узагальнено існуючі методи нелінійного аналізу для дослідження динаміки слабких розв’язків класів неавтономних еволюційних задач з негладкими, розривними або багатозначними функціями взаємодії. Отримано апріорні оцінки та встановлено топологічні властивості розв’язків класів досліджуваних задач. Встановлено теореми про існування, регулярність та структурні властивості граничних циклів розв’язків класів нелінійних еволюційних задач. Досліджено довгострокову динаміку функцій стану нелінеаризованих математичних моделей керованих процесів та полів різної природи, які підпорядковуються негладким суперпотенціальним законам.
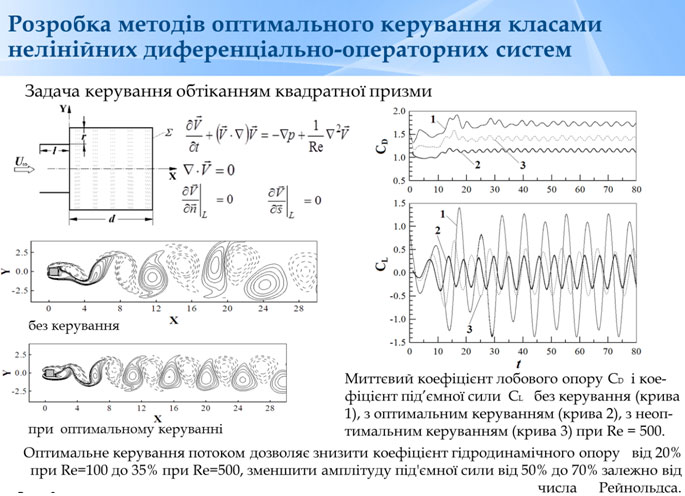
Розроблено нові та узагальнено існуючі апроксимаційні методи розв’язання задач керування для еліптичних та параболічних систем рівнянь з частинними похідними з особливостями в коефіцієнтах диференціальних операторів та з нелокальними крайовими умовами. Досліджено задачу оптимального керування для нелінійних вироджених еліптичних задач з керуючими матричними коефіцієнтами в головній частині диференціального оператора, у тому числі з анізотропним р-Лапласіаном та крайовими умовами Діріхле. Запропоновано та обґрунтовано апроксимаційні методи розв’язання вказаної нелінійної задачі оптимального керування з виродженням в головній частині диференціального оператора. Запропоновано пасивну керуючу схему для оптимізації гідродинамічних характеристик квадратної призми; знайдено оптимальні параметри керуючого пристрою.
Створено комплекс взаємопов’язаних нелінійних моделей розподільчих систем, що враховують видобуток, прокачування, зберігання та споживання енергетичних ресурсів, а також можливість перерозподілу навантаження за рахунок оптимізації основних параметрів мережі. Побудовано алгоритми оптимального розподілу ресурсів із застосуванням методів нелінійного програмування та декомпозиційно-ієрархічних схем.
| Attachment | Size |
|---|---|
| 689.26 KB |




