The formalization of complex methods of nonlinear analysis and optimal control for complex distributed systems of different nature
The new methods of nonlinear analysis to study the dynamics of weak solutions for non-autonomous evolution problems with nonsmooth, discontinuous or multivalued functions are developed. A priori estimates are obtained, and the topological properties of solutions are justified. The theorems on the existence, regularity and structural properties of limit cycles for classes of solutions of nonlinear evolution problems are established. The long-term dynamics of state functions for nonlinearized mathematical models of controlled processes and fields of different nature with nonsmooth superpotential laws is investigated.
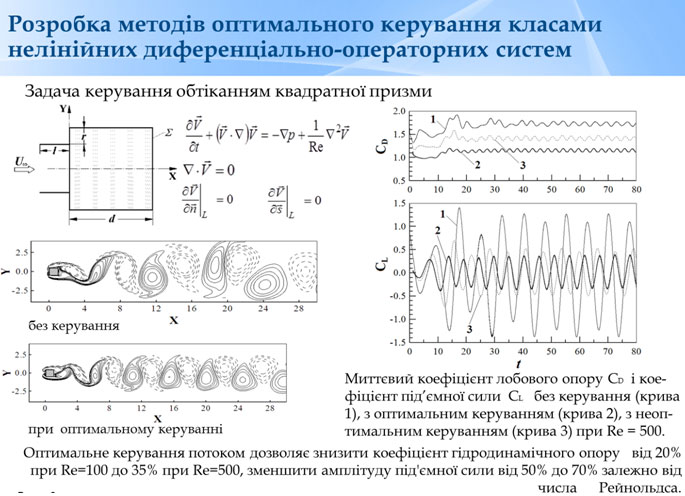
The new approximation methods for control problems solving for elliptic and parabolic systems with partial differential equations in the critical coefficients and differential operators with nonlocal boundary condition are developed. The problem of optimal control for nonlinear degenerate elliptic problems with control matrix coefficients in the main part of a differential operator, including anisotropic p-Laplacian with Dirichlet boundary conditions is investigated. The approximation methods of solving for the nonlinear optimal control problem with degeneration in the main part of a differential operator are proposed and justified. A passive control scheme to optimize the hydrodynamic characteristics of a square prism is developed; the optimal parameters of control device are obtained.
A complex of related nonlinear models of distributed systems, that take into account the production, pumping, storage and consumption of energy resources is developed. The possibility of redistributing the load by optimizing the basic network settings is obtained. The algorithms of optimal distribution of resources using methods of nonlinear programming and hierarchical decomposition schemes are built.
| Attachment | Size |
|---|---|
| 689.26 KB |