Применение стохастических, статистических и функциональных методов для анализа асимптотического поведения случайных полей
Суть работы заключается в исследовании асимптотического поведения случайных полей и функционалов от них, а также применении полученных результатов в теории случайных процессов, статистики случайных процессов, математическом анализе и математической физике. При решении поставленных задач были получены следующие результаты.
Для обобщенных множеств восстановления установлены усиленный закон больших чисел и закон повторного логарифма в терминах включений множеств и в метрических терминах, использую метрики Хаусдорфа и Фреше-Никодима. Кроме того, получена функциональная предельная теорема в смысле сходимости по распределению.
Для случайных зарядов получен равномерный усиленный закон больших чисел. Приведены применения полученных результатов к случайным мерам, порожденным суммами случайных величин, меченым точечным процессам и стохастическим интегралам.
Исследован класс псевдорегулярных последовательностей с невырожденными группами регулярных точек. Для таких последовательностей получены некоторые аналоги свойств функций правильного изменения. Проведено сравнение свойств псевдорегулярных функций и последовательностей, установлены определенные различия. Кроме того, в работе рассмотрены определенные классы функций, которые обобщают псевдорегулярные, и получены интегральные представления типа Караматы для таких функций.
Для неоднородного стохастического дифференциального уравнения с разделением стохастических и детерминированных переменных достаточно общего типа получено асимптотическое поведение решений в терминах параметров уравнения. Результаты применяются к задачам об асимптотическом поведении некоторых конкретных уравнений финансовой математики.
Для заданных последовательностей 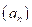 и
и 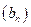 и заданной функции f найдены условия, при которых функция f сохраняет эквивалентность последовательностей в смысле
и заданной функции f найдены условия, при которых функция f сохраняет эквивалентность последовательностей в смысле 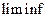 , , то есть условия, при которых из соотношения
, , то есть условия, при которых из соотношения 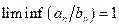 следует соотношение
следует соотношение 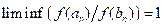
Исследовано предельное поведение сумм элементов линейной авторегрессионной последовательности в терминах полной сходимости и сходимости связанных с ней рядов Сюя-Роббинса-Эрдеша-Спитцера-Баума-Каца. Получен полный аналог теорем Сюя-Роббинса-Эрдеша и Спитцера, а также некоторые частные случаи теоремы Баума-Каца. Кроме того, установлен усиленный закон больших чисел для сумм элементов авторегрессионной последовательности в форме Колмогорова-Марцинкевича-Зигмунда.
Получено обобщение свойства слабой консистентности оценок Коенкера-Бассета в линейной модели регрессии с нелинейно преобразованным гауссовским стационарным временным рядом и сингулярным спектром в качестве случайного шума.
Получено новое достаточное условие, при котором обобщенные решения параболической начально-краевой задачи для системы Петровского с однородными начальными условиями Коши, являются классическими. Условие формулируется в терминах принадлежности правых частей задачи некоторым анизотропным пространствам Хермандера.
| Attachment | Size |
|---|---|
| 325.04 KB |




